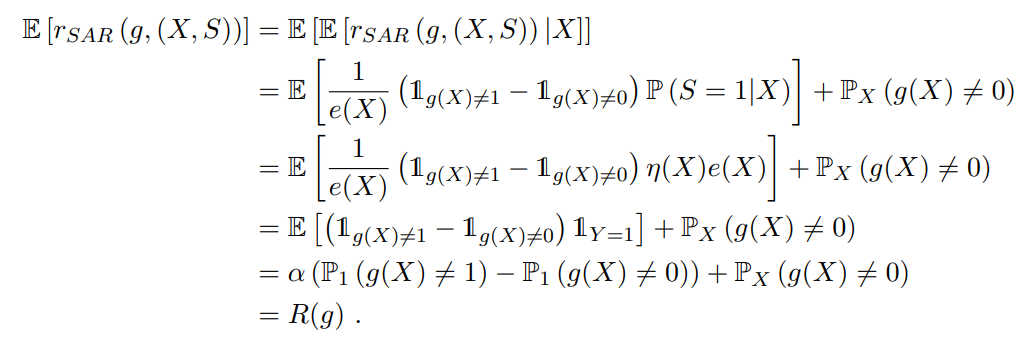Sen(Qian)’s Memo

Risk bounds for PU learning under Selected At Random assumption

Positive-unlabeled learning (PU learning) is known as a special case of semi-supervised binary classification where only a fraction of positive examples are labeled. The challenge is then to find the correct classifier despite this lack of information. Recently, new methodologies have been introduce…

https://arxiv.org

PUの利用例として、病院での診断、機械のデザインの補助、スパム検出、テキスト分類、遺伝病検出、異常検出などがある。機械における疲労設計では、テストを行うが、壊れたをPositive壊れなかったをUnlabeledとして扱うほうがいいね(壊れなくても疲労テストの時間を延ばせば壊れるかもしれないので)。

PUの今までの手法については、📄2020-Survey-Learning from positive and unlabeled data: a survey を参考するとわかりやすい。ここにある2 steps techniqueは経験的には良い結果が得られるが性能の保証はなされていない。

それ以外は基本的には、Cost-sensitiveと言って導き出した式を最小化するというものである。そこでは基本的には、Selected Completely At Random(SCAR)、どの $y=+1$の点でも、ラベルがつく $s=+1$の確率は常に等しいという仮定である。

だが、SCARが適応できない場合が多い。選択バイアスがある以上、Selected At Random(SAR)という仮定も考えられている。そこでは、各点が選ばれる確率は一様ではない。

誤差の上界はMcDiarmidの不等式などを使うことで、訓練サイズ $n$としたら、 $O(1/\sqrt{n})$のオーダで減ることが知られている。さらに、「決定境界から遠いほど、より確実にそのクラスに属する」Margin Assumptionを元にすればもっと精密に $1/n$のオーダにすることができるらしい。

Case-Controlシナリオについて、du Plessisらの研究によって、上界のオーダは $O(1/\sqrt{n_P} + 1/\sqrt{n_U})$であるとわかっている。npはpositiveの数、nuはunlabeledの数。

この研究では、Single-Training-Setにおける、選択バイアスがある=SAR条件下でのリスク上界を評価している。Noisy Labelにも対応しているのがすごいところ。

PN Learningにおけるcost-sensitiveの問題設定。 $\mathbf{x}$に対して、 $y=+1$がPositive、 $y=0$がNegativeだとする。$\pi=p(y=+1)$とすると、以下のように指定のデータ $\mathbf{x}$について、正しく分類できた確率をこのように分解して書くことができる。

最終的な目標は

$\eta(x) = p(y = +1 | \mathbf{x} = x)$、つまり指定されたデータ $x$が与えられたときに、Ground Truth LabelがPositiveである確率を設定する。(これ自体ベイズ分類器といってもいいが　多分これは重回帰しているかな？)単純ベイズ分類器 $g^*$は以下のように定式化できる。 $1/2$以上となったらラベルが付く感じ。

ベイズ分類器における最適の $g^*$(最も正確に表すことができている分類器　所属してるモデルを問わず一番よいもの)との誤差を示すために、以下のようにexcess riskを定義する。

だが、真の $\pi$も $p(\mathbf{x}|y=0)$なども知りようがないため、実際はよさげなモデルを使っていくことになるし、損失関数 $R$も経験的に与えられた訓練データから計算するので、 $\hat{R}$となる。つまり、あらかじめモデル $\mathcal{G}$を指定したうえで、経験的な損失 $\hat{R}$においての最適というのが考えられ、次のようになる。

これを加味したとき、excess riskは次のようになる。 $g^{\mathcal{G}}$は真の損失関数 $R$における、モデル $\mathcal{G}$での最適な分類器。

前半はStatistical Error, 後半はApproximation Errorという。後半はどうしようもないとして、前半のStatistical Errorの最小化を頑張りたいと考える。(なので、真の $g^*$もこの際 $g^* \in \mathcal{G}$に入ってるものとする)

また、この$l(\hat{g}, g^*)$は真の損失 $R$を介して、 $p(\mathbf{x}|y=0)$にも依存し、そして $\hat{g}$の由来のように訓練データにも依存している。(それはそうだ)

Statistical Errorの $R(\hat{g})-R(g)$の収束について、以下のようにVC次元で評価した式が成り立つ。参考資料はこちら。 $p \sim \mathcal{P(G)}$は、真の確率 $p(\mathbf{x}|y=0)$がわからない以上、どんなものであってもその中での最大値、という意味である。

$C_1$は定数であり、 $V$はVC次元。

これをさらに拡張して、 $\eta$が中心の1/2からすべての入力 $x$について、 $y=+1, 0$のサンプルを問わず、常に少なくとも $h>\sqrt{V/n}$だけ離れているとする。

マージンの $h$が大きくなるほど、分類がしやすくなり、収束率が $1/n$まで上昇する。しかし、 $h<\sqrt{1/n}$ならば、この章の最初の式で評価するほうがよくなる。つまり収束率は $1/\sqrt{n}$になる。

これをこの論文の証明ではしっかり使っているので重要だ。

PUでは、ラベルがついているは $s=+1$、ついてないは $s=0$である。ラベルがついているのならば、必ずPositiveである、でもある。 $1=p(y=+1|\mathbf{x}, s=+1)$

ここで、propensity scoreというものを導入する(先行研究2019 Bekkerらが因果推論から持ってきたやつかな)。Ground Truth LabelがPositiveだとわかっている各点に対して、ラベルがつく確率というものである。

下の式は、Negativeがラベルがつく確率はないということである。

ここで、 $\eta(x) = p(y=+1|\mathbf{x}=x)$とすれば、実際にデータ $\mathbf{x}$に対してラベルがつく確率の $\hat{\eta}(x)$は以下のように書くことができる。最後の式変形は、ラベルがつくならば必ず $y=+1$であることを利用した。

ラベルがつく確率は上記のように、propensity scoreと真のPositiveである確率の積から成る、というものだ。

SCARでは、すべての $y=+1$のサンプルは一様に選択されるので、 $e(x)=c(定数)$といえる。このことから、 $p(\mathbf{x}|y=+1,s=+1)$は常に同じ定数である。

選択バイアスがあるとき、 $e(x)$はみな同じになるわけではない。これが難しいところ。

昔から試された手法としては、 $s=+1$をPositive、 $s=0$をNegativeとしてPN Learningする(重みづけを変えるとかして)というのがある。この時学習を重ねるとうまく $p(s=+1|\mathbf{x}=x)=\hat{\eta}(x)$を学習できるだけだが、我々が欲しいのは $p(y=+1|\mathbf{x}=x)=\eta(x)$なので、そもそも収束対象が違うわけだ。

だが、収束対象が違うといっても、PU Learningの学習はノイズには十分にrobustである。Canningsら(2020)が示したように、以下の条件で、 $\hat{\eta}(x)$を予測する不偏学習器は、根本的に違うものを予測したにもかかわらず、 $\eta(x)$に収束するとね。

気持ちとしては、 $\hat{\eta}(x) = e(x) \eta(x)$の式で、 $\eta$の結果からそもそもがPositiveであるデータに対して、式の乗算結果が1/2を超える=ラベルがつくと判定されることができれば、そりゃ収束するよねというもの。

つまり、この条件さえ満たすことができれば、クッソ雑な昔ながらの $s=+1$をPositive, $s=0$をNegativeの分類器で学習させても正しく学習できるってことだ！(効率は知らないが)

この条件下では、分類が難しい= $\eta(x)$が1/2に近いようなものに対しては、propensity scoreの $e(x)$は1に十分に近くなければならないということも示している。また、条件たちを総合すれば、propensity scoreは $\eta(x)$の可動域を考えると、

こうなり、Positiveの各サンプルに対して、絶対にpropensity scoreは1/2以上という意味でもあるわけだ。

ここで、SAR仮定に立ち返って考えてみる。観測が難しいデータほどpropensity score $e(x)$が低くなるので、観測が難しいPositiveのデータに対して $e(x)\geq 1/2$となることはできない。

なので、上の条件は役に立つようには見えるけどいうほどたたないってそれ一番言われているから。これよりも汎用性の高い式を見つけてから、収束率などの評価をしたほうがいいのではないか。

SCARでは、 $\forall \mathbf{x}$にて、 $e(\mathbf{x})=e_c$の定数で表せた。

🚫 Post not found でDu Plessisら示してるように、Case Controlシナリオでは、以下のように分類失敗する確率=リスクを書くことができ、これを $s=+1, 0$のデータだけで書き直せるとした。

ここで、 $l$は2つの引数が同じならば0、そうじゃないならば1を返す01損失だとすれば、全体における分類ミス率は $R(g)$となる。実際は代替損失でやるしかないが。

この式の形から見れば、 $s=0$をNergativeとして扱い、 $s=+1$はPoisitiveとNegativeの両方として扱っていて、そのうえで重みをつけて処理しているという扱い。

ここで、 以下のように書き直せる。

よって、経験的に $R(g)$を求めるのは、SCARでは以下のように行うことができる。

ここまでの話を踏まえると、SCARでのリスク最小化では、クラス事前確率 or propensity scoreが必要。

2019 Bekkerらの論文にあった、Propensity Scoreを用いた最小化。

SARではさらに仮定が必要になる。先行研究では

• 2018 He $e(x)$は $\eta(x)=p(y=+1|x)$から見て、増加関数である。
• 2020 Bekker, 2021 Gong　はPropensity Scoreをパラメトリックなモデルから推測する。

この論文では、2020 Bekkerの方法を拡張して、 $s=+1$のサンプルについてのみ、Propensity Scoreがわかっている状態でのSAR仮定の下でのPU learningについて考えている。割と限定的じゃないか、と思うかもしれないが意外にそうでもない。

まず、Bekkerらも示した、上の $\hat{\eta}(x)=p(s=+1|\mathbf{x})=p(s=+1|\mathbf{x}, y=+1)p(y=+1|\mathbf{x})=e(x) \eta(x)$をもとに代入すると、損失関数は以下のようになる。

さきほどの定数だった $e_c$を代わりに定数ではない、Propensity Score functionの $e(\mathbf{x})$にしただけである。これを経験的に得たものを $\hat{R}_n^{SAR}$とする。 $n$個のデータを用いてる感じ。

Bekker2020らは、$\hat{R}_n^{SAR}$と $\hat{R}_n$との誤差上界を評価していたらしい(読み直す)が、この論文ではさらに一歩進んで、$\hat{R}_n^{SAR}$と真のリスク関数 $R$との誤差上界を評価したい。

下のように、$\hat{R}_n^{SAR}$は $R$の不偏推定量である。

だから、 $s=+1$のサンプルのPropensity Scoreさえ正しく知ることができれば、SARでも真の $R(g)$に近づくことが、できるんですよね(真理)

今までの話の流れを踏まえて、この論文で語っていきますよ。SAR仮定の下でのね。

モデル $\mathcal{G}$に含まれる識別器の中で、経験損失 $\hat{R}_{n}^{SAR}$について、以下のように最適なものを学習によって得ることができる。

そして、理想の $R(g)$との差をと定義する。

Bekkerらは $\mathcal{G}$が有限集合であるときの、誤差の上界の評価を行った。この論文では、無限集合に拡張したうえで、propensity score function $e(x)$の影響も加味したものの証明となっている。

無限集合になったとしても、 $\mathcal{G}$が無限集合であろうとも、VC次元が無限ではないのであれば扱うことができるのだ。

また、separabilityという仮定があり、モデル $\mathcal{G}$に含まれる関数列 $\{g_i\}_{i=1}^k$があって、すべての訓練データについて、以下の式のようにその関数列で理想的な $g$へと収束することができるとする。

分類タスクの難しさを明示的に示すため、Excess Riskの上限を考えたい。この時、以下のように $|2 \eta(x) -1|$を基準にして考える。

ここでの $x$はすべて　$y=+1$のサンプルだと考えているので、最低でも $\eta(x)=p(y=+1|x)$は1/2以上でなければならない。

この仮定を論文の中ではMassartマージン仮定という。2006 Massartの提案したものに基づくらしい。

指定のモデル $\mathcal{G}$と $n$個の訓練データサンプルを与えられたとき、もっともリスクを減らせる識別器 $\hat{g}_{PU}$を考える。

理想の リスク関数をとるような$g$へ収束するある関数列 $\{g_i\}_{i=1}^k$があり、Massartマージン仮定によって、 $\eta(x)=p(y=1|x)$が $|2\eta(x)-1| \geq h$を満たすとする。この時、誤差上界は以下のようになる。

$\kappa_1$は何かしらの定数。 $e_m$はすべてのありうるデータに対して、 $p(k=+1|x,y=+1)$の下界。

この定理からは、 $h\geq\sqrt{V/n e_m}$を満たすのならば、誤差の上界は $O(\frac{V}{n h e_m})$となる。そうではない場合は、 $O(\sqrt{\frac{V}{n e_m}})$となる。

これは普通の二値分類におけるMassart 2006と似ている。 $e_m=1$となっているときはすべての $y=+1$のサンプルが $s=+1$であるということなので、二値分類のと同じ結果になる。逆に、 $e_m$が低いのならば、上界は大きくなってしまう。

この結果からもわかる通り、PU Learningは $e_m$の存在があることから、PN Learningと比べて上界を悪化させることになる。ラベルがつくPositiveが多いほど上界が抑えられるし、だからラベルが大してつかないとPU Learningは難しくなる。

先ほどの学習では上界を見つけたが、これは $\hat{g}_{PU}$についてのもの。本当にこれが最適な識別器なのか？を示したい。

Minimax Riskとは、最悪のサンプルを与えられたときの、最良の分類器を訓練した時のrisk。次のように書ける。つまり、先ほどの下限と考えていい。

このMinimax Riskの上界に関しては、明らかに先ほど導出した以下の式である。

では下界はどうなっているのか？

VC次元 $V \geq 2$だとして、 $n e_m \geq V$だとする。SCARなので、 $e(x)=e_m$とする。ある定数 $\kappa_2$によって記述できるとする。

$n e_m$は全体の中で占めるラベル付きの例の数。このことから、 $\hat{g}_{PU}$は正しい選択だったとわかる。

次の仮定を考える。

どんな小さな値でも、 $e_m$にそれを足せば propensity score function $e(x_i)$はそれ以下となるような、VC次元 $V$だとすると $V$個のサンプルを必ず見つけられる。

この過程を満たす限り、SAR仮定でも、同様にSCAR仮定と同じようなMinimax Riskの下界を得ることができる。